I’ve heard from a few people who are interested in my online journal course – so sorry that I took it down. What was happening is I wasn’t getting enough income to support the course on the platform that I had created it on. So right now I am working on an alternative approach. Hang tight and I’ll get the word out as soon as it’s up and running!
Category: innovation
The “Wounded Healer” Archetype in the PBL Teacher
I have been doing a lot more work with teachers this year as I am not in the classroom. I love watching people teach and talking to them about their teaching. It is clearly a passion for so many people and the modeling of lifelong learning has been so inspirational for me and their students.
One issue that seems to arise in all PBL classrooms, no matter how progressive the teacher, is this feeling that they need to somehow, someday really just not allow the students to be frustrated. Even those who buy into the whole PBL, student-centered, productive struggle pedagogy – deep inside they understand the belief from their own education, that math is black-and-white there needs to be some resolution that is acknolwedged and /or provided by the teacher.
I was talking to a friend about this dilemma a while ago (thanks @phiggiston!) and saying how interesting it is to me that a teacher’s belief from their past can, in the moment, while teaching, often override their beliefs in the current pedagogy. In other words, if a teacher has not experienced independent learning as needed in PBL, it is extremely difficult to not give into the impulse to “save” the students from that feeling of struggle or unease.
Well, coincidentally, @phiggiston has a background in both religious work and in psychotherapy training, so the first the he says to me is, “it’s kind of like the patient-therapist relationship in a way.” And I’m thinking, my teaching is nothing like being a therapist, but of course, I listened intently. I guess there is a Jungian theory that says that “sometimes a disease is the best training for a physician.” In fact, Jung goes as far as to say that
“a good half of every treatment that probes at all deeply consists in the doctor examining himself, for only what he can put right in himself can he hope to put right in the patient.”
_____________________________________________________________________________
So what does this mean for PBL teaching? I had to think of this for a while and also read some Jung as I am not up on the psychological theories that connect to education. I wasn’t quite sure that this “Wounded Healter” achetype paralleled the PBL teacher as much as I originally thought. Here are some points:
- Jung says that for the wounded healer the therapeutic encounter should be regarded as a dialectical process It’s not just I’m going to the doctor and she’s going to tell me what wrong with me. There needs to be some kind of dialogue in order for a real healing to happen. In the classroom, I would argue that this is true about the teacher-student relationship. Traditionally, it has been that not having dialogue would result in learning that was not as long-lasting, effective and/or connected to the students own ideas. It is pretty clear that the PBL teacher needs to create the dilectical process in order for the best learning to happen.
- Jung argues that the physician must help create a safe space where the “patient’s “inner healer” is made available to her unconsciously.” At the same time the physician, should let go of the way she is activiated by the same wounds. This idea is extremely relevant in the PBL classroom. Why do we want to make students comfortable and relieve their anxiety about mathematical learning? My take would be because we hate the way it makes us feel. Knowing that struggle is all to close in our memory can actually help us hand over the power to “heal themselves.” If we can get over that feeling, it will become more of the norm in the classroom.
- There are risks to this type of teaching – the risk of being vulnerable because you are looking at your own wounds, and also looking fragile to the patient (or student). This is a very common concern of teachers who are beginning PBL teaching.
“The experience of being wounded does not make him/her less capable of taking care of the patient’s disease; on the contrary, it makes him/her a companion to the patient, no longer acting as his/her superior.”
In other words, it is worth the experience of creating that open relationship. I go back to Hawkins’ theory of learning (I-thou-It) in which the relationships that exist form a triangle between teacher-student-material.
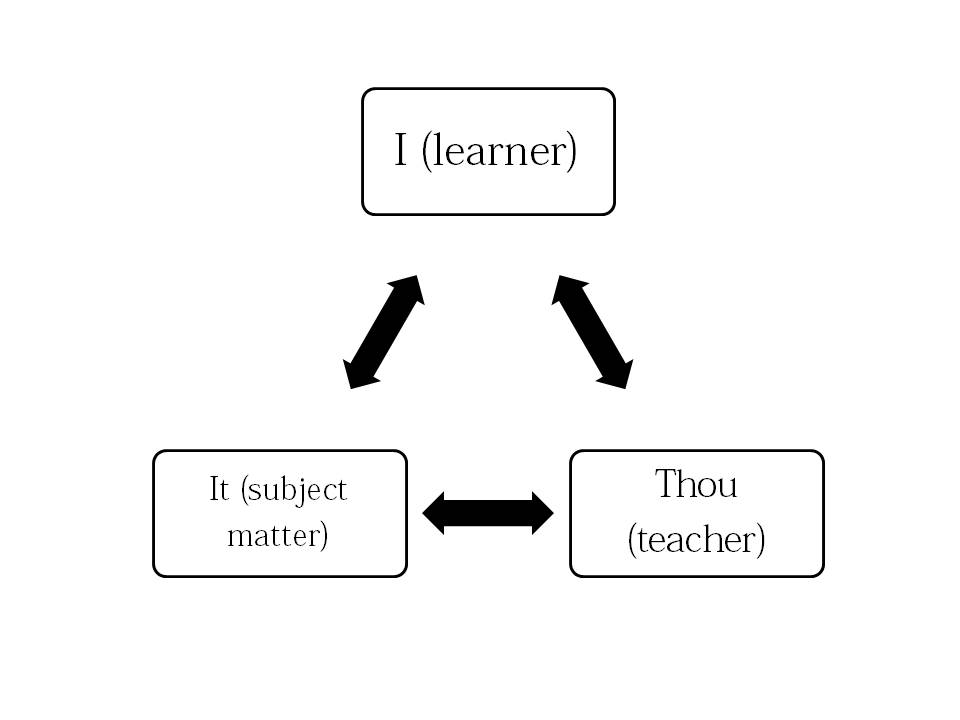
All of these relationships must be nurtured in order for the best learning environment to exist. (For more on this check out Carol Rodgers presentation slides here.)
_____________________________________________________________________________
So does this mean if you did not have this type of experience learning math that you can’t learn to empower your own students in this way? I think not. When I ilook back on my own mathematical experiences many of them were extremely traditionally taught. However, I think what you need to have inside you is both the belief that students are capable of owning and constructing their own knowledge and the ability to create a space that allows them to remain uncomfortable. You have to be willing to let go of your own insecurities and anxieties about learning math and realize that the more you do that, the more the students will feel it as well.
I am currently working on a quasi-research project about this and when/how PBL teachers choose to intervene in class discussion. If there is anyone who is interested in helping me out with this, I’d really appreciate it.
Need Some Help Looking Forward
So I’m trying to figure out how to reach more people and thinking about the future of my professional development plans with PBL for all levels of teachers. I’ve gotten some great feedback from people about the PBL Math Summit so far (from the two years we’ve had it) and I have some ideas about how to create some better online resources too. If you have the time, and are interested in helping me out, would you please fill out this short survey about PD Needs for PBL Math Professional Development. Also, tell others who could give me insights too. Thanks so much for reading my blog and for also being inspired to be interested in PBL math teaching!
Everything Old is New Again…(or why teaching with PBL is so great)
So I heard that what everyone is saying about the new Star Wars Movie, The Force Awakens, is that “Everything Old is New Again” – go ahead google it, there are at least 5 or 6 blog posts or articles about how “BB-8 is the new R2D2” or “Jakku is the new Tattoine” or whatever. I actually don’t have a problem with J.J. Abrams reusing old themes, character tropes or storylines because I think that really great stories are timeless and have meaning and lessons that surpass the movie that you are watching. I still thought it was awesome.
This concept of everything old is new again really hit home to me today in my first period class when I was having the students do a classic problem that I probably first did in 1996 while I was under the tutelage of my own Yoda, Rick Parris (who I think wrote the problem, but if someone reading this knows differently, please let me know). The problem goes like this:
Pat and Chris were out in their rowboat one day and Chris spied a water lily. Knowing that Pat liked a mathematical challenge, Chris announced that, with the help of the plant, it was possible to calculate the depth of the water under the boat. When pulled taut, directly over its root, the top of the plant was originally 10 inches above the water surface. While Pat held the top of the plat, which remained rooted to the lake bottom, Chris gently rowed the boat five feet. This forced Pat’s hand to the water surface. Use this information to calculate the depth of the water.
What I usually do is have students get into groups and put them at the board and just let them go at it. Today was no exception – the first day back from winter break and they were tired and not really into it. At first they didn’t really know what to draw, how to go about making a diagram but slowly and surely they came up with some good pictures. Some of the common initial errors is not adjusting the units or mislabeling the lengths. However, one of the toughest things for students to see eventually is that the length of the root is the depth of the water (let’s call it x) plus the ten inches outside of the water’s surface. Most students end up solving this problem with the Pythagorean Theorem – I’ve been seeing it for almost 20 years done this way. Although I never tire of the excitement they get in their eyes when they realize that the hypotenuse is x+10 and the leg is x.
However, since everything old is new again, today I had a student who actually is usually a rather quiet kid in class, not confused, just quiet, but in a group of three students he had put his diagram on a coordinate plane instead of just drawing a diagram like everyone else did. This intrigued me. He initially wrote an equation on the board like so:
y= 1/6 (x – 0)+10
and I came over and asked him about it. He was telling me that he was trying to write the equation of one of the sides of the triangle and then I asked him how that was going to help to find the depth of the water. He thought about that for a while and looked at his partners. They didn’t seem to have any ideas for him or were actually following why he was writing equations at all. He immediately said something like, “Wait, I have another idea.” and proceeded to talk to his group about this:
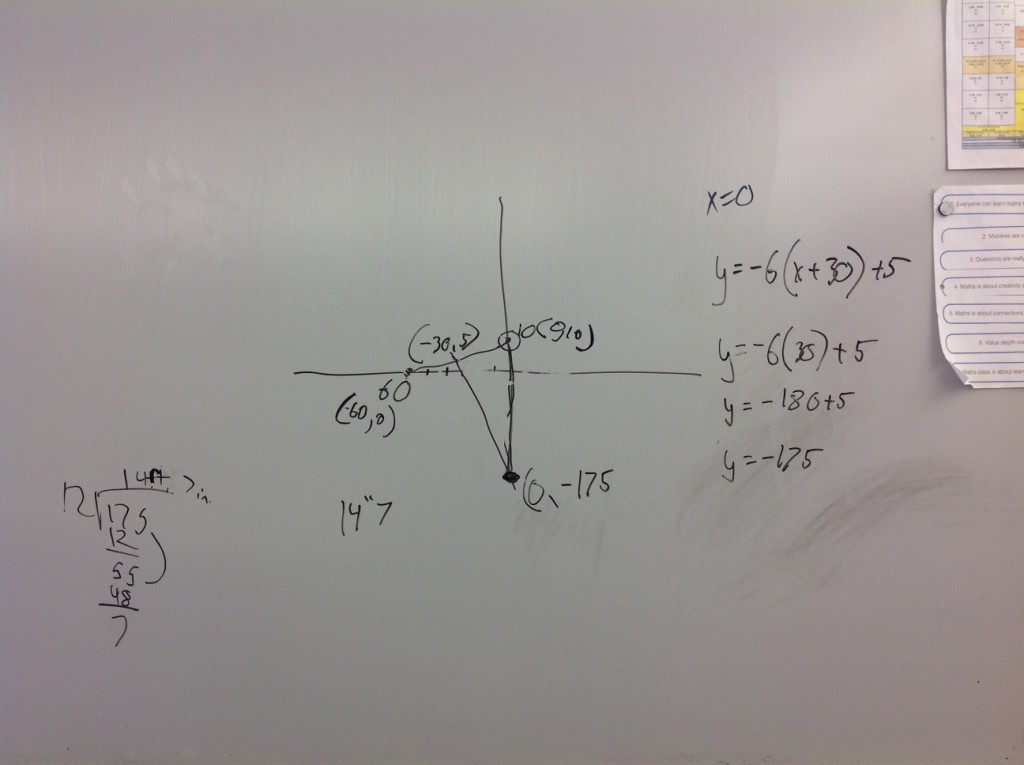
He had realized from his diagram that the two sides of the triangle would be equal and that if we wrote the equation of the perpendicular bisector of the base of the isosceles triangle and found its y-intercept he would find the depth of the water. He proceeded to find the midpoint of the base, then the slope of the base, took the opposite reciprocal and then evaluated the line at x=0 to find the y-intercept. I was pretty impressed – I had never seen a student take this perspective on this problem before.
This made my whole day – I was really dreading going back to work after vacation and honestly, first period was the best class of the day when this wonderful, new method was shown to me and this great experience of this student’s persistence refreshed my hope and interest in this problem. Perpendicular bisectors are the new Pythagorean Theorem!
Why Teachers Don’t Give Feedback instead of Grades, and Why We Should
First in a series of posts about my experiences with “Feedback Before Grades”
Holy Mackerel is all I have to say – Ok, well, no I have plenty more to say – but after about a week and a half of holing myself up with my colleague, Kristen McVaugh, (big shout-out to Ms McVaugh who is not only teaching PBL for the first time but was willing to dive into this amazing journey of alternative assessment with me this year too), I am totally exhausted, almost blind as a bat, partially jaded and crazy – but mostly ready for a drink. This little looped video of Nathaniel Rateliff and the Night Sweats pretty much sums it up…
So here was our well-intentioned plan: we wanted to start the year off with a different type of assessment. I put out my feelers on twitter and asked around if anyone had a rubric for grading assessments where the teacher first gave only feedback and then allowed students to do revisions and then once the revisions were done the students received a grade. Kristen and I knew a few things:
- we wanted to make sure the revisions were done in class
- we wanted to make sure the revisions were the students’ own work (tough one)
- we wanted to give students feedback that they needed to interpret as helpful so that we weren’t giving them the answer – so that it was still assessing their knowledge the second time around
- we wanted to make sure that students were actually learning during the assessment
- we wanted students to view the assessment as a learning experience
- we wanted students to be rewarded for both conceptual knowledge and their skills in the problem solving too
So we created this rubric Initial Draft of Rubric for Grading. It allowed us to look at the initial conceptual understanding the student came to the problem set with and also the initial skill level. Kristen and I spent hours and hours writing feedback on the students’ papers regarding their errors, good work and what revisions needed to be done in a back-handed sort of way.
Here are some examples:
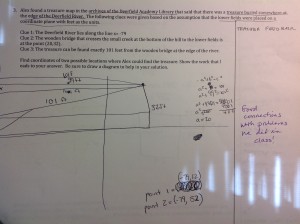
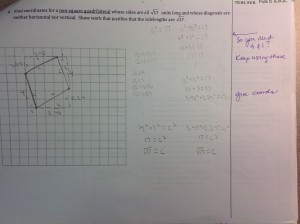
Some kids’ work warranted more writing and some warranted less. Of course if it was wonderful we just wrote something like, excellent work and perhaps wrote and extension question. The hard part was filling out the rubric. So for example, I’ll take Student 3’s work on problem 6 which is the last one above. Here is the rubric filled out for him:
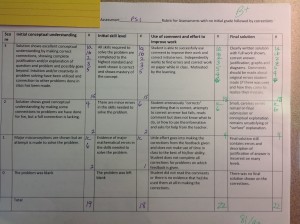
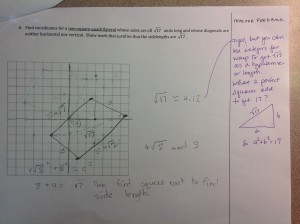
You will notice that I put problem 6 as a 1 for conceptual understanding and a 2 for skill level (in purple). In this problem students were asked to find a non-square quadrilateral with side lengths of sqrt(17). Student 3 was definitely able to find vertices of a quadrilateral, but he was unable to use the PT to find common lengths of sides. I gave him feedback that looking at sqrt(17) as a hypotenuse of a right triangle (as we had done in class) would help a bit and even wrote the PT with 17 as the hypotenuse in the hope of stimulating his memory when he did the revisions.
The day of the revisions Student 3 was only capable of producing this:
He followed my direction and used 4 and 1 (which are two integers that give a hypotenuse of 17, but did not complete the problem by getting all side lengths the same. In fact, conceptually he kind of missed the boat on the fact that the sqrt(17) was supposed to be the side of the quadrilateral altogether.
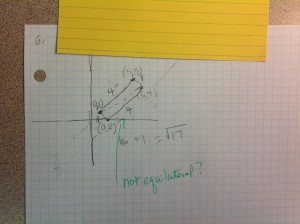
One success story was Student 2. She also did this problem incorrectly at first by realizing that you could use 4 and 1 as the sides of a right triangle with sqrt(17) as the hypotenuse but never found the coordinates of the vertices for me. I gave her feedback saying there might be an easier way to do this because she needed vertices. However, she was able to produce this:
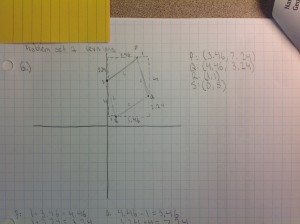
Although she did not give me integer-valued coordinates (which was not required) and she approximated which officially would not really give sqrt(17) lengths it came pretty darn close! I was impressed with the ingenuity and risk-taking that she used and the conceptual knowledge plus the skill-level. Yes, most other kids just used some combination of 1’s and 4’s all the way around but she followed her own thought pattern and did it this way. Kudos to student 2 in my book.
Next time I will talk about some of the lessons we learned, other artifacts from the kids’ work and what we are changing for next time! Oh yeah and some great martini recipes!
PBL & James and the Giant Peach: Try looking at it a different way
James Henry Trotter: “When I had a problem, my mum and dad would tell me to look at it another way.” (Roald Dahl)
I’ve always thought that PBL fostered creative problem solving as opposed to memorization of pneumonic devices. One of my students today proved me right when I gave a “quick quiz” on the use of the idea of tangent. We had discussed tangent in class for only two days and in two ways – one as a slope of a line with a given angle and from that idea we discussed how it could be interpreted as the ratio of the sides of a right triangle (if you put a right triangle under the line).
Of course, during this conversation some student who had studies the ever popular SOHCAHTOA before mentioned this in class and told everyone that they had just memorized this and that’s how they knew it. I said that’s fine but I’d like them to try to think about the context of the problems and see if this helps make any sense of it for them.
So today on the quiz one student was attempting this problem – very basic, very procedural, not at all something that I would call atypical of a textbook-like problem on tangent.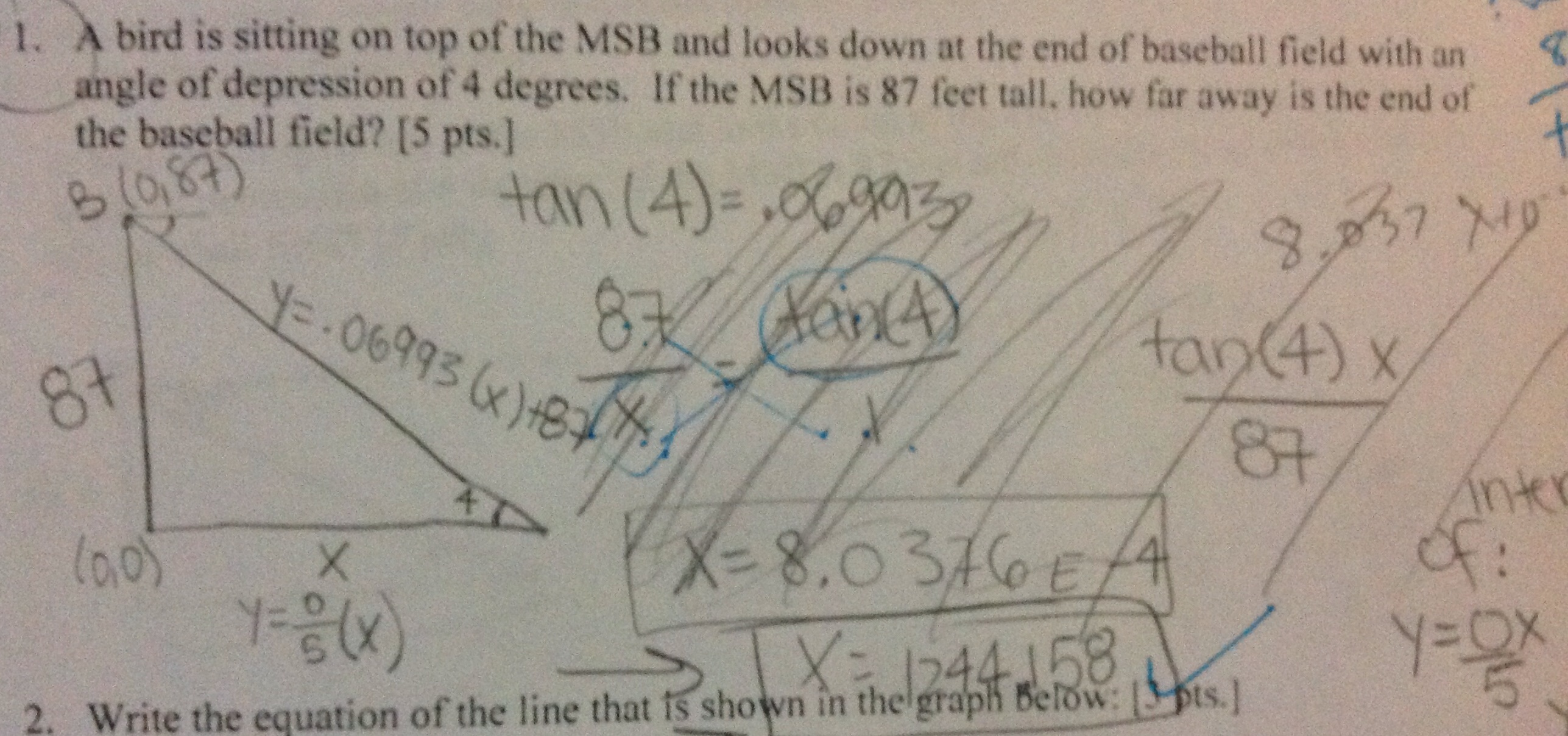
A bird is sitting on top of the Main School Building and looks down at the end of the baseball field with an angle of depression of 4 degrees. If the MSB is 87 feet tall, how far away is the end of the baseball field?
So the student attempts to create a ratio with the sides of the triangle and even sets it up correctly. However, because she does the algebra incorrectly, she gets an answer that is extremely small 8.037 x 10^-4. In fact, during the quiz, she calls me over and asks what it means, she doesn’t remember scientific notation and starts getting all anxious because we didn’t do anything like this in the problems in the previous two days? How can the answer be that small? I said well, you better go back and think of something else.
In most classes, a student in this situation might stress out, try to do the problem over again with the limited perspective of “TOA” or of just viewing the right triangle in one way. However, because this students had also learned other students’ perspectives of tangent as slope of a line what this girl did at this point was to see it from a different way. Interestingly, this is what she did. In an alternative, albeit confusing way of writing the equation of the x-axis, she wrote y=0x to represent the ground. Then she found the tangent of 4 degrees and used that as the slope of a line. She put the bird at the point (0,87)
She writes the equation y= – (tan4)x + 87 and explains that this is the equation of a line that makes a 4 degree angle with the x axis and has a y-intercept of 87. Then she realizes that if she finds the intersection of that line and the x-axis, she would find how far the building is from the baseball field. This is what she does and uses her graphing calculator to get the right answer.
When she hands in this quiz to me, I half expected that tiny little answer as her distance to the baseball field. But what I got was an amazingly inventive solution and a correct answer. With a problem that didn’t make sense, she looked at it a different way and ended up getting the right answer. It was amazing what changing your perspective could do and this was great evidence that even under pressure, the habits of creativity and connection were paying off.
Top 5 Recommended Readings for PBL Teachers Part 2
So, I finally got this done and I’ll continue with the top three readings that I just found extremely useful in my teaching last year.
3. The Innovators’ DNA: by J. Dyer, H. Gregersen and C. Christensen
I rarely recommend books that I have not read yet, but this one is actually on my list to read next so I am recommending it because everything about it just feels right to me. Again, this is not an education book, but a book that is really for business people. The research that was done in preparation for writing this book was looking to see what characteristics people who are viewed as transformative innovators in the business world all share. The authors have come up with five major traits or behaviors that innovators share –
- associating
- questioning
- observing
- experimenting
- networking
You can read a wonderful summary of this book at this link, but I would highly recommend the book as well. It is our job as progressive educators and teachers of PBL to teach these skills. If it isn’t obvious to us already, as PBL teachers, I’ll say it again – that PBL is custom-made for teaching these types of skills which clearly is what this book is stating employers are now looking for.
One thing that I do not read enough of is how PBL encourages the skill of associating. I write a lot about this in my blog and researched it in my dissertation. In fact, connection is one of the main themes that came out in my research that students enjoyed about PBL. The skill of associating is a major skill that is extremely important to innovation and in fact, Steve Jobs in quoted as saying, “Creativity is connecting things.” Allowing students to practice making those connections themselves is key in order for students to practice their own creativity, especially in mathematics.
2. The Five Elements of Effective Thinking by Ed Burger and Michael Starbird
This little gem, published in 2012, was the focus of Ed Burger’s key note address at the 2012 NCTM Annual conference. He actually didn’t try to sell the book too much, but focused on the idea of teaching effective thinking (so then, yeah, I went and bought the book – what can I say, he’s a great speaker). As I was reading through it, all I could think about was how relevant it was to teaching mathematics with PBL. If every student in a PBL classroom took to heart every one of the five elements that are put forth in this book, the classroom would be so much more effective (as would any classroom).
So Burger and Starbird but forth these five elements of effective thinking:
- Understand Deeply
- Make Mistakes
- Raise Questions
- Follow the Flow of Ideas
- Change (which they call the Quintessential Element)
So, you might ask – what’s so great about those? I know this? Well, it’s not those five that are so great – if you are a PBL teacher you probably are already telling your students these already. What I think is so great about this book are the pieces of advice that Burger and Starbird give for each of these five elements. In each chapter, these are not only examples from their own teaching but actual ways to promote each of these elements not only individually but in your classroom as well. The anecdotes that are shared in the book are not only heart-warming but as a teacher you can see how you can make them useful in your own practice.
The combination of deliberately stating these five (and adding CHANGE as the most important) is really key for PBL. Students may know that you want them to understand deeply and in order for them to do that they need to raise questions about their own understanding, but if you don’t constantly and deliberately create a culture for them and you in your classroom it is not a message they will receive seriously.
And the best book, that I would highly recommend reading:
This book, in my opinion, is what PBL is all about. Whether you teach in a school that uses a problem-based curriculum, uses text books and is trying projects, or if you are just trying to create a more student-centered approach to your teaching – this book is getting at the heart of what is creating a change in our schools nationwide. It is why there is a huge movement going on with teachers in our nation trying to find something different to do in their classrooms. Thomas and Brown describe this movement as a shift from a “teaching-centered culture” in our nation’s schools to a “learning-centered culture” which may be the most important shift in education since organized schooling began in the U.S. altogether.
This shift is based on the idea that knowledge is flexible (yes, the idea of Truth with the capital T does not exist – shhhh, don’t tell anyone). Even in mathematics, the way that we solve problems and even the mathematics that we teach students – which topics are “most important” today- is changing rather regularly. This has become so much more clear and visible because of not only the Internet itself, but our access to it. Thomas and Brown suggest that we must be willing to admit that what is most important about education now is not what we teach in schools, but how students learn. Can a student learn in the collective? Are they able to harness different modes of inquiry? Do they experiment in their learning? This shift in the purpose of schooling is not really new to teachers but to our society it is major. Teachers need to learn how to make this switch and articulate the deliberateness of what they are doing in their classroom in order to focus on the shift. (By the way, this also has major ramifications for teacher educators).
I love the five dispositions that will help construct the new culture of learning (very applicable to a PBL environment!)
- Keep an eye on the bottom line (ultimate goal is to improve)
- Understand the power of diversity (strongest teams are rich mix of talents and abilities)
- Thrive on change (create, manage, seek out change)
- See learning as fun (reward is converting new knowledge into action)
- Live on the edge (explore radical alternatives and innovative strategies, discover insights)
All of this is so relatable to my own classroom and curriculum. The more I create problems and experiences that allow my students do have these dispositions, the more I know that I am fostering the “culture of learning” instead of a traditional culture of “teaching.”
So that’s it. My top 5 list of readings for PBL teachers – please let me know what you think and if you end up utilizing any of these authors’ ideas. I know that I have been invigorated by these readings and hope that you will be as well! Have a happy and fulfilling 2014!
Top 5 Recommended Readings for PBL Teachers of 2013 Part 1
Happy New Year! It’s been a busy end of 2013 for me. I’ve been doing a lot of reading and catching up with some writing. So, the New York Times came out with their top 75 Best-Selling Education Books of 2013 and some of them are really great reads and some are just books that are commercially hyped education jargon. I’ll let you read it for yourself and see which you think are which. But this inspired me to think about what I would recommend as great reading for PBL teachers in terms of mathematics. It’s not always easy to get inspired to continue with PBL so I am always on the look-out for good reads and things that might help me to find ways to motivate students in the classroom. I also hate those lists from articles that seem to have all the answers but then when you read them nothing is ever really black and white like “To Flip or Not to Flip: that is the Question” or “5 Resolutions to Modernize Your Teaching For 2014” or “Top 100 Tools for Learning in 2014” – geez, does anyone just write about one thing anymore? Or even give critical analysis of why these are the reasons to flip, or an argument as to the top 100 tools – anyone can make a list.
Including me! So here goes nothing – well, I mean something. I tried to put together some good reading that emphasizes the skills that are needed for working with students in a problem-based classroom. One of the things I hear most from teachers is not necessarily how to work with the curriculum, but how to get students working with each other and how to foster the type of classroom community (curiosity, openness and risk-taking) that is needed in order for students to want to be engaged.
5. The Mistake Manifesto: How Making Mistakes Can Make Us Better by Alina Tugend, 2011.
I first came across Tugend’s writing when I read her Op-Ed piece in the NY Times while ago, but this essay on making mistakes says so much about Tugend’s great attitude towards how mistakes are not only helpful, but are a wiser and more powerful way of learning. She says that “we do single-loop learning when we need to do double-loop learning.” I love that and I believe that PBL’s method of returning to ideas in its scaffolded and multi-topic approach often allows students to revisit ideas multiple times. Tugend talks about how most of our society creates a fear of making mistakes because we have this idea that we aren’t supposed to make mistakes. This is in turn makes us all risk-averse unfortunately and only allows the most unstructured students and learners to be creative innovators. This is what we have to turn around. Her manifesto doesn’t necessarily tell us how to do this, but it’s a wonderful argument for why we should.
4. Flow, by Mihaly Csikszentmihalyi, 1990
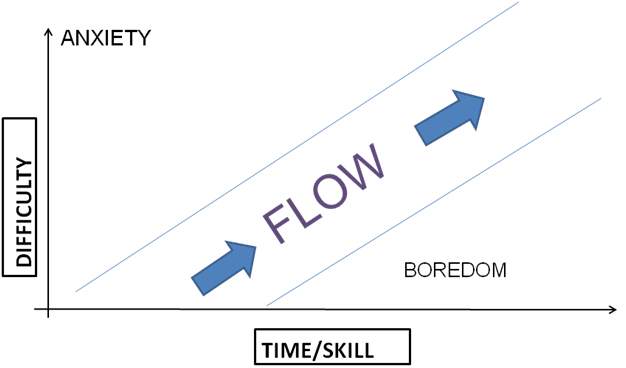
This book’s original intent was to investigate the psychological experience of happiness, however this past year it became connected for me to the process of problem-based learning. OK, so this book is not from 2013 – or even from the past few years, but what happened in 2013, is that I read an article that sent me to this book. The article was called “The Problem-Based Learning Process as finding and being in Flow” by Terry Barrett and it discussed the concept of ‘flow’ (from Csikszentmihalyi’s book) and compared the PBL process (the discourse that occurs, the exchange of ideas and that learning process itself) to the optimization of creativity that occurs in the ‘flow’ process. In this book, Csikszentmihalyi defines ‘flow’ as “the state in which people are so involved in an activity that nothing else seems to matter. The experience itself is so enjoyable that people will do it even at great cost, for the sheer sake of doing it.”(Csikszentmihalyi, p.4). Wouldn’t that be great if that’s the way students viewed learning? One way to see it is like this:
(Barrett, 2013)
The idea being that the state of flow in learning comes when the optimal problem or activity is presented to students such that the difficulty and time or skills given keeps their interest long enough to minimize anxiety and maximize love of learning and the return on their learning (reinforcement of confidence, efficacy, enjoyment, agency, etc.). A lot of the book is based on the idea of the state of flow helping to create the optimal state of happiness so it might not relate directly to teaching, but I highly recommend the last two chapters which are entitled “Creating Chaos” and “The Making of Meaning” which can be directly translated to the PBL classroom and are highly useful for the PBL teacher looking to see how you can create the state of flow for your students.
Tomorrow I will catch up with numbers two and three! (hopefully get you #1 as well)
Buyer Beware…when using rubrics for critical thinking skills
One of my goals in my work is often to help classroom mathematics teachers to be more deliberate in the ways in which they assess problem solving. Although many people can be cynical about rubrics, I think that students can find them at least helpful to know what a teacher expects of them. I have some students who told me that they pull out my rubric for grading journal writing almost every time they go to write a journal entry this fall.
However, a rubric that is vague and ambiguous about expectations can cause more harm than good. Just throwing a rubric around that students can look at, or one that you can post on your website that you can show an administrator and say, “See, I have a rubric for that” isn’t necessarily a good thing. Especially for problem solving. Problem solving as a process is a very difficult thing to nail down for students especially in terms of the levels of how they can improve in their work.
I recently ran across this rubric that posted on a website under the title “Awesome Problem Solving Rubric for Teachers.”
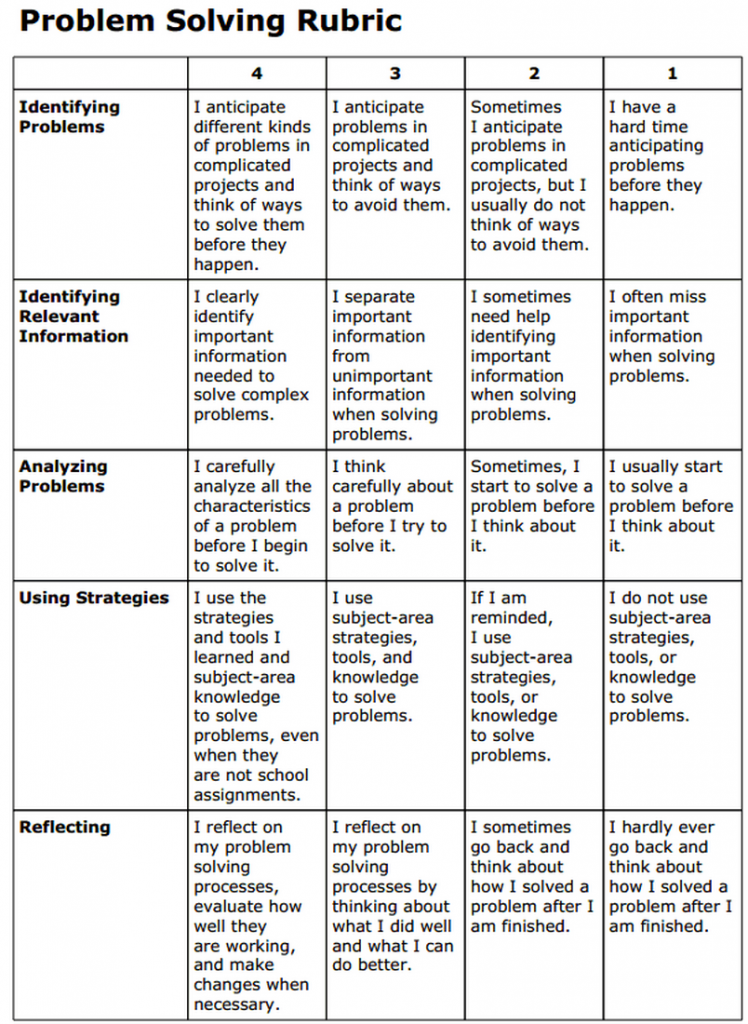
As I read through this, at first glance the categories look pretty good – Identify the problem, identify relevant information, analyze the problem, use strategies and reflect on the process. Sounds like a pretty standard problem solving process –very similar in many ways to Polya’s process or the steps that Jo Boaler discussed in her online course How to Learn Math this summer.
The graded level descriptors of how a student might be able to see where their work “fits” in the rubric seems to only put the behaviors on a “continuum” of Always- sometimes- never instead of trying to describe actions that the student could do that describe a mediocre way of using a strategy. For example, analyzing a problem can be so much more descriptive than just “I think carefully” about the problem before a student starts.
They could:
1. listen deliberately to others’ ideas and reflect on them in writing or verbally
2. question the given information of a problem – does it make sense in a realistic way?
3. think about the representations they can come up with for the problem – does a graphical approach make the most sense? Why? Would making a geometric representation be better, if so why?
4. In comparing a new problem to ones I’ve already done, can I list the similarities and differences? What is this question asking that others I’ve done not asked?
How many students can really ascertain what “thinking carefully” about a problem is? I have found that more and more we need to erase as much ambiguity as possible to help students learn to be critical thinkers. As we feel the need to teach critical thinking, reasoning skills and sense making, it is even more imperative to have rubrics that are as precise as possible.
Now, I don’t claim that mine are perfect, but my rubrics and student feedback forms have gotten some pretty good reviews from teachers and successful feedback from students. I work on them every summer and am continually editing in order to be more deliberate about the feedback I give my students.
I also highly recommend the rubrics from the Buck Institute Website under their “tools” category. I also adapted one of their critical thinking rubrics that was aligned to the Common Core and changed it directly for my PBL curriculum – more for presentation of problems and novel problem solving. I’m still working on it because I have to think about exemplars for what would be above standards, but let me know if you have any feedback.
Critical Thinking rubric for PBL
So, I would just warn anyone to beware of “awesome rubrics” for teachers that they find on the internet because something that might seem awesome at first glance might end up doing more harm than good.
30-Year-Old Wisdom, Not Recent Rhetoric
Recently, the Exeter Bulletin published an amazing Memorial Minute in honor of Rick Parris just this past week which I believe was wonderfully written. In it they use a quote that Rick stated back in 1984 which shows his wisdom and insight into student learning of mathematics and the basis of my interest in PBL.
“My interest in such problems is due in part to the pleasure I get from working them myself, but it also stems from my belief that the only students who really learn mathematics well are the ones who develop the staying power and imagination that it takes to be problem-solvers. Such students will have thus learned that being accomplished in mathematics is not simply a matter of learning enough formulas to pass tests; that creative, original thought requires living with some questions for extended periods of time, and that academic adventure can be found in the pursuit and discovery of patterns, more so than in the mere mastery of known formulas.”
In this one paragraph is the whole of what you can find in so many blogposts, writings of so-called “experts” and “thought-leaders” in education nowadays. I’m not so sure that the recent trend of promoting curiosity, innovation, creativity, perseverance and ‘grit’ are such original ideas. It just has taken a long time to catch on in any type of mainstream educational jargon.
Rick Parris knew the truth over 30 years ago and led the charge in curriculum writing, pedagogical study, and leadership in student learning. Always humble, but deeply interested in discussion, he would never shy away from the chance to discuss teaching mathematics and so I was lucky enough to have him as a colleague in the early years of my career. He helped form my teaching philosophy and I owe a huge debt to the wisdom he imparted to me. I seek to help students “live with some questions” every day in my classroom and I join them daily on the “academic adventure” of problem-based learning. I can only hope that the mathematics community and society as a whole in the U.S. can catch up with his wisdom and we can eventually change the way we view learning mathematics.