Category: Agency

Having Students Be More Aware of their Contributions in PBL

One of the things I do at the middle of the term to have students reflect on the way that they talk about mathematics in class, is have them evaluate their work with my Student Self-Report on Class Contribution and I give them detailed feedback on their rankings of each type of question and what I think about their work so far.  But what I’ve found in the past is that it’s hard for them to remember specific examples of when they “helped to support the point by contributing evidence” or “raised a problem in another person’s solution” weeks or days after the fact.  Students have so much to think about during a class period that it really needs to be “in the moment” for them to be deliberately thinking about what they are doing and saying to each other.

So I had this idea that I would actually have them keep track of the types of questions and comments they made to each other over a five day period at the end of the term and then hand it in to me.  This way they would check off each category of question or comment at the moment when they did it.  So I made copies of this table of Student Analysis of Contribution and had them keep it on their desks while we were discussing topics or problems in class.  They had to have something to write with while they were talking and taking notes too.

Initially the students were very concerned about how they were going to tell the difference between each of the types of contributions.  But little by little, it became easier.  These categories were not arbitrary, they happened all the time, they just hadn’t really thought about it before.   For example, when a student presented a problem but had made an error and didn’t know it, another student usually “raised a complication in another person’s soltuion” or “pointed out an unspoken assumption or misunderstanding.”  These are important contributions that they were making every day about mathematics and are important critical thinking skills they didn’t even realize they were developing.  I just wanted to help them be more specific about realizing it.

The first day we did this I heard some students say something like, “Ooh, I just…(brief pause while looking at the table)… ‘started the group discussion on a rich, productive track by posing a detailed question.” with pride and excitement (and maybe a little sarcasm).  But after three days of doing it, and students seeing that they had places that they could check off, one student actually said, “I think that this table makes our conversations more interesting.”

Here are some samples of student feedback:

Quiet student who needs to work on all types of comments and questions

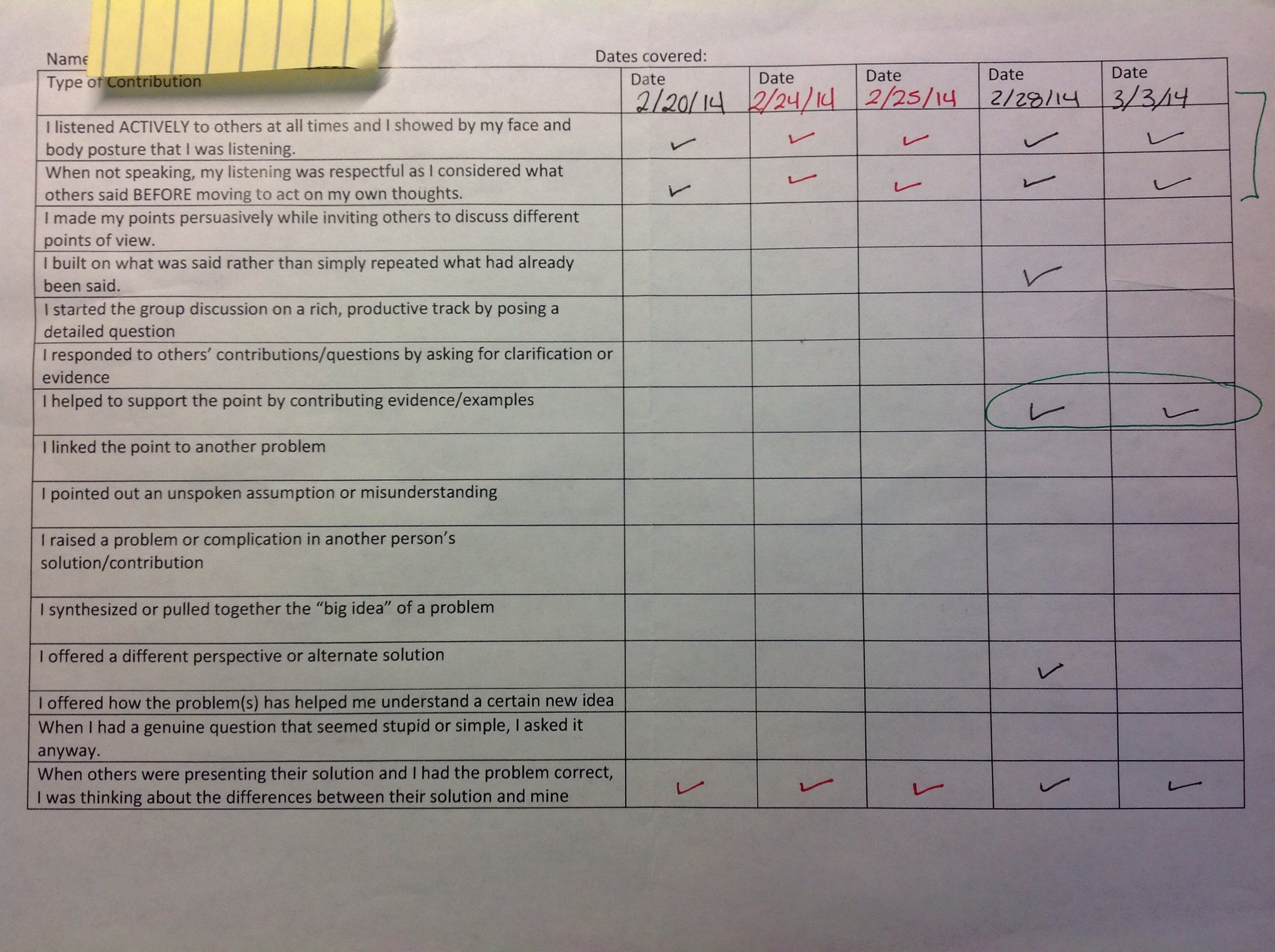
This first respondent is a student is very quiet, and she knows it.  She rarely speaks in class, but is actively listening.  I’ve spoken to her about why she does not ask questions or share her ideas in class and she says that she is afraid of being wrong in front of everyone.  My hope all year has been that seeing everyone else be wrong regularly would eventually show her how acceptable it was in class.  It was clear that using this table showed her that there are many different ways to contribute to class discussion.  When she presented her problems in class (which she will do when asked) she is very capable and knows that she is contributing evidence or examples, but she rarely questions others’ work.  I do remember the time when she “built on” what was said by asking a question about someone else’s solution.  She also sometimes asks for clarification of her own understanding, but I know that she’s capable of more.  I struggle with how to encourage her to get more out of class discussion, but at least now she knows how important a role she can play.

Outgoing student who lacks interaction from other kids

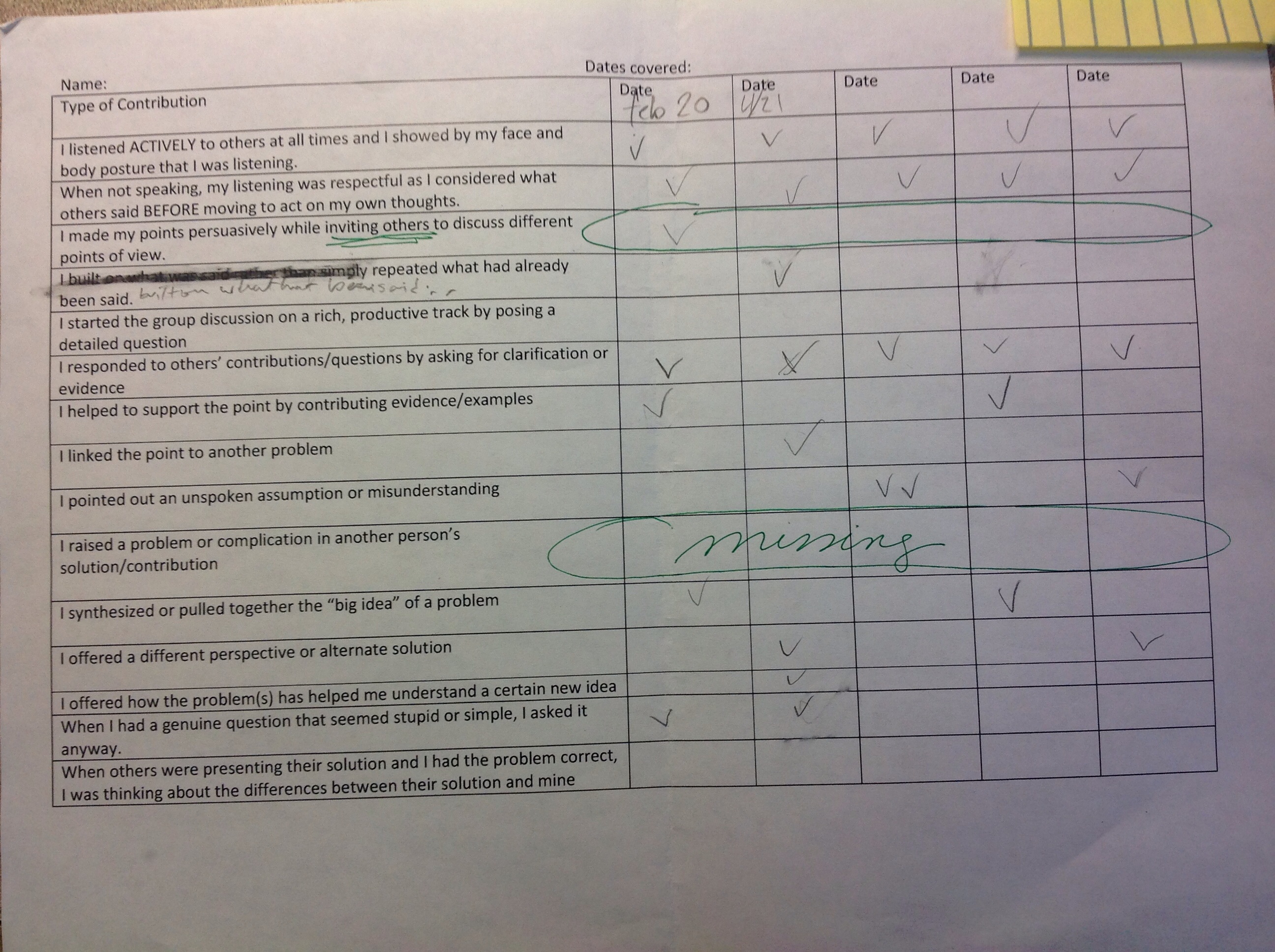
This is a really interesting student who is quite inquisitive and very comfortable with sharing his ideas.  When he has a question or comment, it’s very easy to get him to go to the board and naturally start writing another idea or possible solution method.  However, I noticed was missing in his table were checks in the two rows that had to do with “inviting others” into his thought process and also making comments on others’ solutions and ideas.  It made me wonder how much time in class he spends listening to other students talking or if he is just listening to his own ideas in his own mind.  I am working on trying to get him to collaborate more – with his creative mind it would behoove him to start interacting more with others.

Outgoing student who is unaware of his effect on others

This table belongs to a student who really has overestimated his contributions to class.  He definitely spends a lot of time talking (and hence I spend a lot of time managing his unrelated talking unfortunately) and thinks that talking – any kind of talking – is useful and contributing to class discussion.  One of the things I have talked to him about is the idea of active listening and how important not speaking can be.  He has not yet caught onto the idea of being respectful while listening, and still is considering his next talking move while others are trying to make their points.  It will be a difficult discussion, but a necessary one for this young man to grow in important ways.  At least I now have this chart to refer to when I have that discussion.

So was this exercise everything I had hoped?  Not really – but it definitely had some great highlights.  Class discussion was very exciting and interesting while students were aware and deliberate knowing the different types of ways in which they could contribute.  Knowing that they had to hand this table in to me in 5 days was putting the onus on them to show that they had or had not fulfilled what I had observed of them in class.  I do believe they learned a lot about what they were capable of.  I do believe I would do it again.

Does journaling in PBL promote resilience?

So I just read a great blogpost by Kevin Washburn of Clerestory Learning entitled “Teaching Resilience: Reflection” and it immediately made me think of the Metacognitive Journaling that I have students do in my classes.  I never really thought of it the way that Washburn was describing the reflection and the conseuences of reflection, but it’s pretty clear that if his theory is right, that a by-product of journaling could easily be resilience.

Initially, Washburn talks about the process of reflection – right out of Dewey in a way – but he narrows it down to the steps in the process (but does mention the word metacognition – thinking about thinking).  He defines reflection as “the ability to monitor one’s own thinking” which is what I tell my students the goal of writing in the journal is.  Hopefully, by the end of the year, they will have realized the way they look at problems and how they’ve had those “lightbulb” or “ah-ha” moments enough after writing about them, that when they come across a new problem, the process of being aware of their own problem solving is much more natural.

Washburn’s three steps are as follows:

1. Asking yourself “what am I thinking now?”
2.  What can I tell myself to redirect my thinking?
3.  What can I do differently?

Most students in the beginning of the year, can easily do the first step – it begins very simply as them just redoing their work (usually the correct way), which can, unfortunately, just be them rewriting their notes from class.  However, this has to be a place to start for them.  This is where teacher feedback is key.  I spend most of my time writing comments like ,”I want to hear what *you* did initially” or “is this what your first thoughts were?”  It’s really hard for students to believe that you want a record of what they did wrong.

But somewhere during the year, kids grow in their understanding of WHY their initial idea didn’t work.  This seems to be the most important part of the reflection.  That gained insight gives them not only deeper understanding, but a sense of ownership and responsibility for their own learning that can’t be had with just seeing how many points they got off from the problem on an assessment.

I’ve written about this a few times (see other blog entries) and have seen kids grow in their understanding during the 18 years that I’ve been using journals in my classroom.  However, what Washburn helped me see is how this skill of recognizing how their initial erroneous thinking has actually made them a stronger, more confident thinker.  This is an amazing gift.  As Washburn says,

“In life and in the classroom, the one doing the thinking is doing the learning. When thinking ceases and self-defeating messages crescendo, we can guide students to healthier states of mind and, in the process, equip them to make such cognitive turns on their own.”

So  great!

PBL & James and the Giant Peach: Try looking at it a different way

2 Comments

James Henry Trotter: “When I had a problem, my mum and dad would tell me to look at it another way.” (Roald Dahl)

I’ve always thought that PBL fostered creative problem solving as opposed to memorization of pneumonic devices.  One of my students today proved me right when I gave a “quick quiz” on the use of the idea of tangent.  We had discussed tangent in class for only two days and in two ways – one as a slope of a line with a given angle and from that idea we discussed how it could be interpreted as the ratio of the sides of a right triangle (if you put a right triangle under the line).

Of course, during this conversation some student who had studies the ever popular SOHCAHTOA before mentioned this in class and told everyone that they had just memorized this and that’s how they knew it.  I said that’s fine but I’d like them to try to think about the context of the problems and see if this helps make any sense of it for them.

So today on the quiz one student was attempting this problem – very basic, very procedural, not at all something that I would call atypical of a textbook-like problem on tangent.

A bird is sitting on top of the Main School Building and looks down at the end of the baseball field with an angle of depression of 4 degrees.  If the MSB is 87 feet tall, how far away is the end of the baseball field?

So the student attempts to create a ratio with the sides of the triangle and even sets it up correctly.  However, because she does the algebra incorrectly, she gets an answer that is extremely small 8.037 x 10^-4.  In fact, during the quiz, she calls me over and asks what it means, she doesn’t remember scientific notation and starts getting all anxious because we didn’t do anything like this in the problems in the previous two days?  How can the answer be that small?  I said well, you better go back and think of something else.

In most classes, a student in this situation might stress out, try to do the problem over again with the limited perspective of “TOA” or of just viewing the right triangle in one way.  However, because this students had also learned other students’ perspectives of tangent as slope of a line what this girl did at this point was to see it from a different way.  Interestingly, this is what she did.  In an alternative, albeit confusing way of writing the equation of the x-axis, she wrote y=0x to represent the ground.  Then she found the tangent of 4 degrees and used that as the slope of a line.  She put the bird at the point (0,87)

She writes the equation y= – (tan4)x + 87 and explains that this is the equation of a line that makes a 4 degree angle with the x axis and has a y-intercept of 87.  Then she realizes that if she finds the intersection of that line and the x-axis, she would find how far the building is from the baseball field.  This is what she does and uses her graphing calculator to get the right answer.

When she hands in this quiz to me, I half expected that tiny little answer as her distance to the baseball field.  But what I got was an amazingly inventive solution and a correct answer.  With a problem that didn’t make sense, she looked at it a different way and ended up getting the right answer.  It was amazing what changing your perspective could do and this was great evidence that even under pressure, the habits of creativity and connection were paying off.

Encouraging Student Voice without Knowing It

I’d like to think of myself as a master teacher.  I’ve always thought of myself as very aware of student perspectives in my classroom, but today after a weekend of being in bed with a bad cold, all I wanted to do was get through the problems and get back home – I admit it.  I was not being very reflective and deliberate in my teaching.  However, even with all that, something amazing happened today.  Of course, I’d like to take all the credit, but I have to say I think the credit goes to the method of PBL, relational pedagogy and the students in my class.  So here’s what happened.

We had gone through about half the problems and I think they could tell I was in a pretty bad mood.  We got to one of my favorite geometry problems that starts an interesting strand of thinking that has to do with which polygons tessellate with others.  One girl goes to the board (I’ll call her Robin) and she presents her solution to this problem:

The diagram at the right shows three regular pentagons that share a common vertex at P.  The three pentagons do not quite surround P.  Find the size of the uncovered acute angle at P.

So Robin does what I expect (and in my fuzzy state of mind I am just happy that someone knows what’s going on).  She writes on the board:

Her argument being that the three angles in the pentagons were congruent since they were all regular and the leftover part would be the difference between those three and 360.  So, I was ready to move on.  She was right, after all?  Let’s go and do the next problem.  But no, Tye speaks up and says, “Hey that’s what I got but that’s not what I did.  That’s so cool I got the right answer.”  So, as tired and sick as I was, I said, “What did you do Tye?”  He says all I did was do 108 divided by 3 and it worked!”  He was so proud of himself.  I sat there and was like, OK, this isn’t going to fly, but I was so exhausted that ….but wait, another student says, “Hey that’s cool.  You just take the angle measure and divide it by how many polygons you have.” I’m thinking, oh no, this is gonna get out of hand fast….

Then another student says, “wait a minute, lets see if it works with hexagons: ”  So before they  know it they realize that it can’t work with hexagons and Helen says, “but that’s because there are too many, you need something with room left over, like a square.  What if you only use 3 squares? Is the angle leftover 90 divided by 3?”

So they soon have disproved the theory that if they just take the number of interior angle of the regular polygon and divide by how many polygons there are and divide them, they’ll get the leftover angle.  But Tye is still adamant that he’s all proud he got the right answer.  I am, however, still struggling with the fact that he can’t justify to himself why it works.  I say,”Listen, why don’t you think about it some more and we’ll come back to it?” but guess what, they don’t let it go.

Luke says, “Well, what I did was just draw a triangle down there.”

He says that he knew that empty space was really an Isosceles triangle and because the base angles were supplementary to the interior angles of the pentagon, he could find the angle at the top.  At this point, I’m like “will this ever end? Will I be able to get some Tylenol?” (I know can you believe me?  what a role model…)  A few other kids really liked what Luke did and said they did that too and thought they had been wrong, but now see that it was a valid method.  I mean, could I ask for more?  This was awesome stuff going on!

So at this point, we move on and do a few more problems, but then towards the end of class, I notice there are about three kids who aren’t really paying attention to the problem at hand.  I couldn’t figure out what was going on because they are usually right in the thick of our discussions.  So finally, one girls practically yells (and I mean, with arms flailing and everything) “I got it!”  Alanna had been working on a justification for Tye’s idea of dividing the interior angle by three the whole class period, as had two other students.  It was so interesting a problem to them that they just couldn’t stop.  Alanna said, “I knew they were vertical angles, but I just couldn’t see how they could be the same.”  She and the two other students had been playing with some isosceles triangles and vertical angles and come up with this solution:

By finding that the base angles of the isosceles triangles on the sides were both 36, and that the one in the middle was also 36, they had seen the reason why Tye could just divide 108 by 3.  They knew it wasn’t just pure luck that it worked and it made them all so happy.  It was so satisfying and I could just feel the excitement in the room.

It was so funny to me because everything that I did to try to discourage them from going to that place of curiosity or demanding the reason didn’t help.  They went there anyway. Their voices were heard – again and again.  The culture that we had set was there and no matter what I did now, at this point in the year, they knew what was expected of them – asking questions, not giving up, being inquisitive & creative.  This class helped me realize that even on my bad days I need to see each student for who they are and be just as excited for each of them to realize their own potential.  And if I don’t have the energy or strength to push them through, maybe, just maybe, they will.

Being Inspired & About Intuition

In early January, I had the good fortune to go down to the NCSSM Teaching Contemporary Mathematics Conference in Durham, NC.  There were many wonderful speakers there including Dan Teague, Maria Hernandez, Gloria Barrett and the Key Note Speaker on Saturday morning, Gail Burrill.  Gail spoke about making up tasks and lessons that actually allowed students to ask good questions that made them think mathematically.  She gave many wonderful examples and talked a lot about the responsibility of the teacher to probe and use the following pedagogical strategies:

The tasks we give and questions we pose should ensure that students:

  1.  are actively involved in choosing and evaluating strategies, considering assumptions, and receiving feedback.
  2.  encounter contrasting cases- notice new features and identify important ones.
  3. struggle with a concept before they are given a lecture
  4.  develop both conceptual understandings and procedural skills
(National Research Council, Adding it Up (2001) and How People Learn (1999) From Burrill’s Presentation)
She also gave this wonderful rubric for Inquiry Math Tasks

It made me realize that because I use a PBL curriculum very few of the problems that we look at are actually full inquiry (or student-generated). Although what happens in class is that students will create questions that I think are wonderful and a lot of discussion stems from those questions.

It will be a whole other blogpost for me to detail how problem-based learning fosters every one of those in a meaningful way.  It really blew my mind when I was sitting there listening to her.  I was thinking,”This is an amazing framework to describe to people what PBL is like.”  In fact, at one point she said that she believe that all mathematical tasks should be done where students “work alone a bit, and then they share.”  I thought that is exactly the pattern of grappling with problems for homework and then sharing ideas the next day in class.  Gail never prescribed any methods or told anyone to follow any specific guidelines, but just stated these general ideas.  It was a wonderful talk.

Later on that morning, I gave a talk on teaching BC Calculus with problem-based learning.  Perhaps I made a comment too many about how I was against “teaching to the test” and a young man asked a question in defense of the AP Calculus exam itself.  He felt that the multiple choice section allowed students to learn or develop intuition about questions and problem solving and that the benefits of practicing such repetitive type questions was to gain that type of intuition for those topics and those questions.  Well, I hope I am remembering this question well enough, but I would argue that intuition for problem solving and intuition for problems is two different things.  There have been many mathematicians and mathematics educators throughout time from Polya to Alan Schoenfeld who have attempted to structure problem solving or how to teach problem solving to anyone.  From my readings, there is always a “reflection” step where you compare your ideas in the “novel” problem solving process (novel being the key word here, being something that you have not yet seen).  My argument being that repeating the same type of problem definitely ensure that on a test with the same type of problems you may be able, under pressure, to answer those problems correctly.  Does it show that you have developed an intuition on what to do in those types of problems?  Perhaps.  It might show that you have differentiated between the different types of outcomes of those problems.  Does it show that you understand that concept or that you understand what the question is asking?  I am not sure.  I have worked with enough students who have mastered the art of eliminating answers in a multiple choice scenario to know that it does now show understanding, but intuition about answering the question.

However, I do think that having a student practice problem solving in a way where you are faced with a novel problem on a regular basis (perhaps nightly – along with other problems that they have seen before) where they are asked to try something new and reach into their prior knowledge and write down what they think they might be able to do allows them to practice creativity, risk-taking, connection and sharing those ideas.  After a long period of time of doing this, it would seem that some type of intuition becomes habit and they develop more knowledge about mathematics overall. More importantly, “Students are thus engaged in the creation of mathematics, allowing them to see mathematics as a part of human activity, not apart from it.”  I believe that’s why PBL in mathematics is even more important than in other disciplines and that we need to change the culture of the classroom before asking more from our teachers and students.

Using Journal Writing in PBL

1 Comment

Over the years, especially in PBL with mathematics, I have found that students greatly appreciate the authorship and ownership that comes with keeping a journal in my classroom.  In fact when I asked my students earlier this year, “When do you feel most confident in this class?” and here are some of the feedback responses they gave me:

“When I am about to hand in a journal.”
“When I am writing a journal entry because there are various concepts that initially don’t understand, and after discussions I make big discoveries and therefore it makes writing about it easier for me.”

There is something that I have come to appreciate about the way students grow to be able to show how they understand a concept.  Recently, I read a student’s journal entry and thought it was so amazing that I asked him if I could blog about it.  I thought that it really showed how he moved through his understanding of the concept and how he struggled with it to the end. In fact, he presented this problem in class thinking that he had gotten it right and wonderfully, kept going and learned something in the process.

The student – let’s call him Pete- was dealing with a problem that was towards the end of a thread that dealt with the concept of distance – distance between two points, distance between a point and a line, distance between two lines, etc.  This question was asking students to think about two different types of distance.  Here’s the problem:

“Plot all of the points that are 3 units away from the x axis and write an algebraic expression for those points.  Then plot all the points that are 3 units away from the point (5,4) and write an algebraic expression for those points.”

Up until now all we had discussed was writing expressions for Pythagorean distance between two points and writing equations for equations of lines.  We had also talked about the fact that the closest distance from a point to a line is the perpendicular distance.  So Pete was easily able to answer the first part of the question seeing that the set of all points that were 3 units away from the x axis were both the line y=3 and the line y=-3.  He drew a diagram discussing his concept of distance from a point to a line and how he visually (in his mind and physically on paper and at the board that day in class – connected them together).

However, in his journal he wrote about how the second part of the question seemed just as easy to him at first.  “I assumed I needed to do a straight line. I then saw ‘three units’, so I put a point on (5,1), and drew the line y=1.  If (5,1) was 3 away, I thought, shouldn’t all the points on the line be 3 away?” Here’s what his first diagram looked like:

Pete’s First attempt

Pete had tried to use his understanding of distance being “three units” away from a point in the same way that being “three units” away from a line in the previous problem.  However, when he was at the board, another student told him they had thought of it another way and shared with Pete something Pete realized very soon…. “Only 1 point on each of the lines was actually 3.  The rest of the points were actually all further than 3 units from the point.”  Here’s his diagram of his realization of that:

Second attempt

So now Pete is discussing how he is using his knowledge of Pythagorean distance and seeing that only the vertical and horizontal points are actually the required 3 units away.  Huh, how does he move forward now?  At the moment when he was in class, it took another classmate to say that ALL the points were supposed to be 3 units away and that he (that classmate) thought it would look more like a circle.  Pete was still determined to correct his own work (which I just love) then attempted this drawing:

 

Third attempt

Pete writes:

“This, I thought, would cause all points on the line to be 3 units away from point (5,4).  However, I was again wrong.  The blue line on the diagram shows a point on one of my lines that was more than 3 units from (5,4). The red line shows a point on one of the lines that is less than three units from (5,4) [it would’ve been great if he went into more detail, but at this point I’m so psyched that he’s going into this much detail!]  The green lines are points that are 3 units away from point (5,4).  I have effectively created a range of lengths from (5,4) opposed to what the question was asking for which was 3 units from (5,4).”

This is some of the most insightful journal writing I’ve ever seen from a high school student.  Pete is moving through his understanding of what it means for a point to be 3 units away from another point (even when another student has imposed their understanding on him) and is trying to show me how he came to understand his classmate’s argument that it is a circle.  Realizing that there are points that are more than 3 units away (farther out than this diamond shape), 3 away (at the vertices) and closer than 3 (along the sides of the diamond)….well, that there was a range and not all constantly 3, showed him that his ideas was not correct.

Pete then draws this diagram:

Getting the concept

After understanding this, Pete writes:

“It made perfect sense!…Any point from the centerpoint of a circle to any point on the circle was the same length (the radius).  I immediately drew the connection.  3 was the radius and (5,4) was the center.  the distance between the middle point and any point on the circle was 3!”

Although Pete didn’t write about the discussion that ensued about the algebraic expression, I still felt like the goals of metacognitive journaling were reached with this entry.  Pete has articulated why he chose this problem to me, he started with his misunderstanding, how another student or the class discussion/experience had helped move him through his understanding and he could clearly write about how he now has a good understanding of the mathematical concept.  I was so proud of Pete.  Yes, it’s true, not every student gets to this point of writing mathematically by January of the school year, but the growth that occurs in each individual student is what is important – not necessarily the level of maturity in the writing.  However, I have learned not to prejudge or dismiss any student who starts off at a lower level because I believe they are all capable of growth.

If you are interested in looking at my grading rubric for journals or asking me questions about how I use them in the course, don’t hesitate to get in touch. (If you are looking for the grading rubric, make sure you scroll to the third page of that pdf).

Does PBL teach Resilience?

I just read a great blogpost by a business writer, Gwen Moran, entitled, “SIx Habits of Resilient People.” When I think of people that I admire in my life for their resilience there was usually some circumstance in their life that led them to learn the quality of resilience because they had to. Even the examples that the author uses in this blogpost – being diagnosed with breast cancer, almost being murdered by a mugger, the inability to find a job – these tragedies that people have had to deal with can be turned into positive experiences by seeing them as ways in which we can learn and grow and find strength within ourselves.

But wouldn’t it be great if it didn’t take a negative experience like that to teach us how to be resilient? What if the small things that we did every day slowly taught us resilience instead of one huge experience that we had no choice but to face? Having to deal with small, undesirable circumstances on a daily basis, with the help and support of a caring learning community would be much more preferable, in my opinion, than surviving a mugging. (Not that one is more valuable than the other). But I just wonder – and I’m truly ruminating here, I have no idea – if it is possible to simulate the same type of learning experience on a slower, deeper scale by asking students to learn in a way that they might not like, that might make them uncomfortable, that asks more of them, on a regular basis.

I think you know what I’m getting at. Does PBL actually teach resilience (while also teaching so much more)? In my experience teaching with PBL the feedback I’ve received from students has been overwhelmingly positive in the end. But initially the comments are like this:

“This is so much harder.”
“Why don’t you just tell us what we need to know.”
“I need more practice of the same problems.”
“This type of learning just doesn’t work for me.”

Having students face learning in an uncomfortable atmosphere and face what is hard and unknown is difficult. Thinking for themselves and working together to find answers to problems that they pose as well as their peers pose is very different and unfamiliar. But does it teach the habits that Gwen Moran claim create resilient people? Let’s see. She claims that resilient people….

1.Build relationships – I think I can speak to this one with some expertise and say that at least if the PBL classroom is run with a relational pedagogy then it is very true that PBL teaches to build relationship. My dissertation research concluded nothing less. In discussing and sharing your ideas, it is almost impossible not to – you need relational trust and authority in order to share your knowledge with your classmates and teacher and this will only grow the more the system works for each student.

2. Reframe past hurts. – If we assume that real-life “hurts” are analogous to classroom mistakes, then I would say most definitely. PBL teaches you to reframe your mistakes. PBL is a constant cycle of attempting a problem->observing the flaw in your solution ->trying something else and starting all over again. This process of “reframing” the original method is the means by which students learn the the PBL classroom.

3. Accept failure – This may be the #1 thing that PBL teaches. I am constantly telling my students about how great it is to be wrong and make mistakes. You cannot have success without failing in this class. In fact, it is an essential part of learning. However, students in the US have been conditioned not to fail, so that reconditioning takes a very long time and is a difficult process.

4. Have multiple identities – In a traditional classroom, certain students fulfill  certain roles – there’s the class clown, the teacher’s pet, the “Hermione Grainger” who is constantly answering the teacher’s questions, etc. But what I’ve found happens in the PBL classroom is that even the student who finds him/herself always answering questions, will also find him/herself learning something from the person s/he thought didn’t know anything the next day. Those roles get broken down because the authority that once belonged only to certain people in the room has been dissolved and the assumption is that all voices have authority. All ideas are heard and discussed. PBL definitely teaches a student to have multiple identities while also teaching them a lot about themselves, and possibly humility, if done right.

5. Practice forgiveness – This might take some reinterpreting in terms of learning, but I do believe there are lessons of forgiveness in the PBL classroom. Students who expect themselves to learn everything the first time and when they don’t, feel stupid, need to forgive themselves and realize that learning is an ongoing process. Learning takes time and maybe needs more than one experience with a topic to see what the deeper meanings and understandings really are. Since PBL is not just a repetitive, rote teaching method, students need to learn how to be patient and forgiving of their own weaknesses as a learner and take time to see themselves as big picture learners.

6. Have a sense of purpose – This habit is about “big picture” purpose and looking at a plan. From the research that I did, I also found that PBL brings together many topics in mathematics, allowing students to see the “big picture” connections between topics much better than traditional teaching does. The decompartmentalization that occurs (as opposed to compartmentalizing topics into chapters in a textbook) is confusing at first because they are not used to it, but eventually students see how topics thread together. Just the other day in my geometry class we were doing a problem where they were asking to find as many points as possible that were 3 units away from (5,4) on the coordinate plane. A student in the class asked, “is this how we are going to get into circles?” The whole class was like “Oh my gosh, it is, isn’t it?” Bam, sense of purpose.

All in all, I feel that PBL meets Moran’s criteria of “resilience characteristics” in ways in which it allows students to practice these habits on a regular basis.  So not only does PBL help students learn collaboration, communication and creativity, but perhaps they will see the benefits over time in learning how to move forward from a setback – just a little.

 

Experimentation, Creativity and Problems

Returning from vacation is always a tough time, but the other day in my honors geometry class, I decided to present them with a problem that had at its heart the Pythagorean Theorem – which we’ve been using since the beginning of the year – and I wanted to see what they would do with it.  So I showed them this video I found on line.  It poses an interesting question regarding buying android tablets and what size you might want.  Before we watched it, I had them search online to compare the prices of some well-known tablet brands and see if there was a major difference in their 7 inch size tablet vs. their 10 inch size tablet.  We came up with some prices that looked like this:

We talked about how, in most cases the price of the 10 inch tablet was about 1.5 or 1.6 times the price of the 7 inch tablet.  Was that reasonable?  Did it make sense?  10:7 was only about 1.4.  So then we watched the video:

Visit NBCNews.com for breaking news, world news, and news about the economy

I posed the question to them, “Do you think what this guy is saying is true?  Is the 10 inch table really twice as big as the 7 inch? If so, what evidence can you give to say that it is and how can we justify whether or not any of these tablets really are?”

Great conversation ensued.  I was so excited.  One group of students started trying to find numbers that the dimensions of the two tablets could be.  Of course, the first thing they assumed was that the one with the 10-inch diagonal screen would have width of 6 and height of 8 (don’t we all just love those Pythagorean Triples?) but then they realized when they did that there could be so many other triangles that could have a hypotenuse that was 10 as well.

Another group started trying to compare the areas of the screens to see if they could find dimensions of two tablets that actually had one area that was twice as big as the other one (that kept the diagonals 7 and 10).  This was an interesting group because they had thought through the concept of “twice as big” but hadn’t made the jump to what it would mean for one to be that much bigger.

I was then called over to a group where a girl was trying to explain her idea of how to make two 7 inch tablets fit into the 10 inch tablet.  I’ll call her Tracy.  Tracy said something like this to me: “If ttwo small ones fit into one of the big one, that would mean that the height of the big one is twice as big as the width of the little one” and she proceeded to go up to the board and draw a picture like this:

This started everyone talking.  It actually became really cool for a while.  They soon realized that you could let the dimensions of the smaller tablet be w and 1/2h while the dimensions of the bigger one were h and w.  This combined with the Pythagorean Theorem allowed them to solve a quadratic system of equations to find the dimensions of both tablets, if it were true that the 10 inch tablet were truly “twice as big” as the 7 inch. (I believe the 10 inch tablet had to be 8.24 inches by 5.65 inches approx).

We were unable to confirm all of this by finding dimensions online so if anyone can do this, please let me know!  But what was the most amazing part of this problem solving exercise for me and my students was the engagement that I observed from their interest in the problem and their own motivation to come up with a way to justify or debunk the claim made in the video.  We are going to write up some paragraphs about their findings and present them to each other next time we meet.

I was very proud of the way they were not afraid to experiment with different ideas initially and how Tracy moved through her own ideas and took risks with the group and those around her, eventually getting her and others to the path that made sense to many of them.  It was really a group effort and worked well.  If anyone else tries this, please let me know how it goes.

Teaching Students to Become Better “Dancers”

So the other day I read a tweet by Justin Lanier that really sparked my interest.

 We all know the scenario in classroom discourse where a student asks a question – a really great question – and you know the answer, but you hedge and you say something like, “That’s a great question! I wonder what would happen if…”  So you reflect it back to the students so that they have something to think about for a little while longer, or maybe even ask a question like “Why would it be that way?” or “Why did you think or it like that?”  to try to get the student to think a bit more.  But what Justin, and the person who coined the phrase “authentic unhelpfulness” Jasmine Walker (@jaz_math), I believe were talking about was hedging because you really don’t know the answer – sincere interest in the uniqueness of the question – not because you’re so excited that student has helped you move the conversation forward, but because of your own excitement about the possibilities of the problem solving or the extension of the mathematics.

I think what got me so excited about this idea was how it connected to something that I was discussing earlier this summer with a group of teachers in my scaffolding in PBL workshop in late June.  In a PBL curriculum, the need to make sure that students have the right balance of scaffolded problems and their own agency is part of what Jo Boaler called the “Dance of Agency” in a paper she wrote in 2005 (see reference).  My understanding of this balance goes something like this:

(c) Schettino 2013

So initially, the student is confused (or frustrated) that the teacher refuses to answer the question although you are giving lots of support, advice and encouragement to follow their instincts.  The student has no choice but to accept the agency for his or her learning at that point because the teacher is not moving forward with any information.  But at that point usually what happens is that a student doesn’t feel like she has the authority (mathematical or otherwise) to be the agent of her own learning, so she deflects the authority to some other place.  She looks around in the classroom and uses her resources to invoke some other form of authority in problem solving.  What are her choices?

She’s got the discipline of mathematics – all of her prior knowledge from past experiences, she’s got textbooks, the Internet, her peers who know some math, other problems that the class has just done perhaps that she might be able to connect to the question at hand with previous methods that she might or might know how they work or when they were relevant – that discipline has had ways in which it has worked for her in the past and lots of resources that can help even if it may not be immediately obvious.

But she’s also got her own human agency which is most often expressed in the form of asking questions, seeing connections, drawing conclusions, thinking of new ideas, finding similarities and differences between experiences and thinking about what is relevant and what is not.  These pieces of the puzzle are not only important but a truly necessary function of the “dance of agency” and imperative to problem solving.

Interweaving both of these types of agency (and teaching kids to do this) have become more important than ever.  Yes, being able to use mathematical procedures is still important, but more important is the skill for students to be able to apply their own human agency to problem and know how and when to use which mathematical procedure, right?  This “dance” is so much more important to have every day in the classroom and if what initiates it is that deflection of authority then by all means deflect away – but the more we can “dance” with them, with “authentic unhelpfulness” and sincere deflection because we need to practice our own human agency, the more we are creating a true community of practice.

Boaler, J. (2005). Studying and Capturing the complexity of practice – the Case of the ‘Dance of Agency’